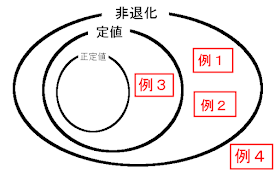
そして、次の図の関係を示す。
以下では実数の集合をRとする。
内積の定義
R 上のベクトル空間 V において、<・|・> : V×V → R の関数がx, y, z ∈ V で a ∈ R のとき
1. 双線形性
- <ax + y | z> = a <x | z> + <y | z>
- <x | ay + z> = a <x | y> + <x | z>
- <x | y> = <y | x>
をみたすとき、(この記事では)内積という。
非退化内積の定義
上記に加えて、3. 非退化性
- ∀z [ <x | z> = 0 ] ⇒ x = 0
をみたす内積を非退化内積という。
つまり
「どんなベクトルと内積をとっても零になるベクトルは、零ベクトルしかない」
という性質をみたす内積である。
3. 非退化性の対偶
- x ≠ 0 ⇒ ∃ z [ <x | z> ≠ 0 ]
ととらえてもよい。これはつまり、
「零ベクトルではない x との内積は、うまくベクトル z を選べば零にならないようにできる」
ということである。
定値内積の定義
1.双線形性と 2.対称性の他に、3.非退化性ではなく、4. 定値性
- <x | x> = 0 ⇒ x = 0
正定値内積の定義
1.双線形性、 2.対称性、そして 4. 定値性の他に、5. 正値性
- <x | x> ≧ 0
この定義から直ちに、内積が正定値であれば、定値である。
定値内積は非退化内積であること
内積が「定値」ならば「非退化」であることを示す。4. 「<x | x> = 0 ⇒ x = 0」と
3.の前件 「∀z [ <x | z> = 0 ]」を仮定する。
3.の前件で特に z = x のとき、<x | z> = <x | x> = 0 である。
よって4.により、「x = 0」が成り立つ。これは3.の結論である。(証明終わり)
以上より、内積が正定値なら定値、よって非退化である。
非退化だが定値内積ではない例
4.定値性の否定は、∃x [ <x | x> = 0 かつ x ≠ 0 ]なので「∀z [ <x | z> = 0 ] ⇒ x = 0」 かつ ∃x [ <x | x> = 0 かつ x ≠ 0 ]
をみたす内積<・|・>が存在することを示せばよい。
例1
簡単のため dimV = 2 とし、定値ではない内積を<e1 | e1> = 1 , <e2 | e2> = 0 (ここが定値ではない) , <e1 | e2> = <e2 | e1> = 1
で定義する。
x = x1e1 + x2e1 , z = z1e1 + z2e2 とすると、(反変ベクトルの成分は添字を上に、基底の添字は下につける慣習に倣った)
<x | z> = x1z1 + x1z2 + x2z1 = (x1 + x2)z1 + x1z2 = 0
これが任意の z で成り立つには、( z1 と z2 についての恒等式なので)
x1 + x2 = 0 かつ x1 = 0
すなわち x = 0
よって非退化である。
例2
よくあるミンコフスキー平面の例。dimV = 2 とし、定値ではない内積を
<e1 | e1> = 1 , <e2 | e2> = -1 , <e1 | e2> = <e2 | e1> = 0
で定義すると、
<x | z> = x1z1 - x2z2 = 0
これが任意の z で成り立つには、
x1 = 0 かつ x2 = 0
すなわち x = 0
よって非退化である。
そして、x = e1 + e2をとると、
<x | x> = 1 - 1 = 0 かつ x ≠ 0
のため、定値でない。
この例から、あるベクトルの大きさは正、あるベクトルの大きさは負となる内積は、<x | x> = 0 となる x を構成できるため、定値でないことがわかる。
定値内積だが正定値ではない例
例3
dimV = 2 とし、内積を<e1 | e1> = -1 , <e2 | e2> = -1 , <e1 | e2> = <e2 | e1> = 0
で定義すると、
<x | x> = - (x1)2 - (x2)2 ≦ 0
であり、この式から
<x | x> = 0 ⇒ x = 0
も分かるので定値だが正定値ではない。
非退化でない内積の例
ついでに、非退化ですらない内積の例を挙げてみる。例4
dimV = 2 とし、内積を<e1 | e1> = 1 , <e2 | e2> = <e1 | e2> = <e2 | e1> = 0
で定義すると、
<x | z> = x1z1 = 0
が任意の z で成り立つとき、 x1 = 0 だが x2 は 0 でなくてもよい。
よって
∀z [ <x | z> = 0 ] かつ x ≠ 0
をみたす x が存在する ( x = e2 あるいは e2 の実数倍) ことがいえたので、非退化でない。
(関連のある記事)
内積が非退化であると、計量テンソルに逆行列が存在することがいえる。それは次回。
0 件のコメント:
コメントを投稿